��ϊ�
�Q�i���˂P�O�i���@/�@�P�O�i���˂Q�i���@/�@�Q�i���̂W�i���@/�@�Q�i���̂P�U�i��
��ϊ�
�Q�i���˂P�O�i���@/�@�P�O�i���˂Q�i���@/�@�Q�i���̂W�i���@/�@�Q�i���̂P�U�i��
�Q�i���˂P�O�i���̕ϊ��͌��̏d�݂��l����
�P�O�i���˂Q�i���͌��̑g�ݍ��킹���l����
�Q�i���̂W�i���͂R�����ŕϊ�����
�Q�i���̂P�U�i���͂S�����ŕϊ�����
2�i��10110��3�{�������̂͂ǂꂩ�B(IP_H21�t_��64)
�A�@111010
�C�@111110
�E�@1000010
�G�@10110000
�����@�E
�������͉��p�^�[��������܂����C2�i�����m�̑����Z���}�X�^�[���Ă���̂ł���C2�i���́u10110�v��3���Ɛ����ɒH��t���܂��ˁB�������C�u�`����ł�2�i�����m�̑����Z�̐����͂��Ă��܂���ł����̂ŁC����̉���ł͕ʂ̉�������������܂��B
�@2�i���́u10110�v��10�i���ɕϊ����܂��B
�����̏d�݂��l���āC1�̂��錅�̏d�݂����v���܂��B����͏ォ��16�C8�C4�C2�C1�Əd�݂�U��ƁC16�{4�{2��22�ƂȂ�܂��B
�A����22��3�{���܂��B
������͂��̂܂�22�~3��66�Ŗ��Ȃ��ł��ˁB
�B3�{����66��2�i���ɕϊ����܂��B
��10�i����2�i���ɕϊ�����ꍇ�́C���̏d�݂̑g�������l���܂��B���̏d�݂͏ォ��C64�C32�C16�C8�C4�C2�C1�ł��̂ŁC64��1��2��1����C66�ɂȂ�܂��ˁB
����āC�u1000010�v�������ł��B
����Ȑ��������ϊ��̎d�����悭�킩��Ȃ��I�Ƃ������́C�u�`������������Ă�����x�ϊ����@�ɂ��Ċm�F���Ă��������B�i��_���G
8�i����55��16�i���ŕ\�������̂͂ǂꂩ�B(IP_H21�H_��64)
�A�@2D
�C�@2E
�E�@4D
�G�@4E
�����@�A
8�i����16�i���̕ϊ��́C2�i�����o�R���ĕϊ�����̂��ȒP�ł��B
�܂�C8�i���́u55�v��2�i���ɕϊ�����B���̕ϊ�����2�i����16�i���ɕϊ�����Ƃ�������ōl���܂��B
8�i���́u5 5�v�����ꂼ��3������2�i���ɕϊ�����Ɓu101 101�v�ƂȂ�܂��B
���ɁC����2�i���́u10 1101�v��������4������16�i���ɕϊ�����Ɓu2 D�v�ƂȂ�܂��B
1101��D�̕ϊ��������������܂��C1101��8�{4�{1��13�ł�����C10��A�C11��B�C12��C�C13��D�Łc�c�Ƃ����悤�ɍl���Ă��������B
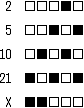
10�i����2�C5�C10�C21�CX���C�܂̏��ڂ̔����Ŏ��̂悤�ɕ\���B���ꂼ��̏��ڂ����̂Ƃ���0�C���̂Ƃ��͏��ڂ̈ʒu�ɂ���Ă��錈�܂����قȂ鐳�̒l���Ӗ�����B���̌܂̏��ڂ̒l�����v����10�i����\�����̂Ƃ���ƁCX���\�����l�͂ǂꂩ�B(IP_H23�H_��72��)
�A�@12
�C�@20
�E�@24
�G�@30
�����@�E
���ꂼ��̏��ڂ����̂Ƃ���0�C���̂Ƃ��͏��ڂ̈ʒu�ɂ���Č��܂����l���Ӗ����邻���Ȃ̂ŁC�e�ʒu�����̂Ƃ��̒l��1�����肵�Ă����܂��B
�܂��u2�@�����������v����u�E����2�Ԗځv��2�ł��邱�Ƃ�������܂��B
���Ɂu10�@�����������v�ɂ��āC�u�E����2�Ԗځv��2�ł�����C�u������2�Ԗځv��10�|2��8�ł��邱�Ƃ�������܂��B
���Ɂu�E����1�Ԗڂ�3�Ԗځv����肵�����̂ł����C���͂���͓���ł��܂���i�O�O�G
�u�E����1�Ԗځv��1�ŁC�u�E����3�Ԗځv��4�ł���H�@�ƂȂ�ƂȂ��l���Ă��܂��܂����C�^�����Ă����炾���ł́C�u�E����1�Ԗځv��4�ŁC�u�E����3�Ԗځv��1�Ƃ����\�����r��������܂���B
�����Ŗڐ���ς��܂��B�u21�@�����������v�Ɓu5�@�����������v���̓����C�u21�@�����������v�̂����C�u�E����1�Ԗڂ�3�Ԗځv�̍��v��5�ł�����C�c��́u������1�Ԗځv��21�|5��16�ł��邱�Ƃ�������܂��B
��������ƁuX�@�����������v�́u������1�Ԗځv��16�C�u������2�Ԗځv��8�Ȃ̂ŁC16�{8��24�ł��邱�Ƃ�������܂��B
�u�`����̓��e�ɂ��Ď��₪����܂��B���̏ꍇ�A�ǂ̂悤�Ɏ��₷��Ηǂ��ł����H
������ɂ��ẮA�u�`����̉��ɂ���܂��uFacebook�̃R�����g�@�\(��1)�v�܂��́uYoutube���̃R�����g�@�\(��2)�v�������p���������B
��������������e�ɂ��ẮA�K�X�AQ&A�ɓ]�p�������܂��̂ŁA�\�߂��������������B
��1 Facebook�ւ̃��O�C�����K�v�ł��B
��2 Youtube�T�C�g�ւ̈ړ����K�v�ł��B