貴方の成長を手助けする無料ＩＴ資格スクール

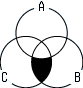
次のベン図の黒色で塗りつぶした部分の検索条件はどれか。(IP_H21春_問71)

ア　(not A) and B and C

イ　(not A) and (B or C)

ウ　(not A) or (B and C)

エ　(not A) or (B or C)

正解　ア

ひとまずAの部分を無視して，BとCにだけ注目します。黒色で塗りつぶされている部分は，BとCの交差している部分ですので，この部分が「B and C」であることが分かります。

次にAをあわせて考えると，「B and C」の部分でAに含まれる部分は白色になっています。

言い換えれば「B and C」でかつ「Aじゃないところ」で，さらに言い換えれば「B and C」and「not A」となります。

よって，これと同じ意味の選択肢のアが正解です。

札幌にある日本料理の店と函館にある日本料理の店をまとめて探したい。検索条件を表す論理式はどれか。(IP_H24春_問69)

ア　(“札幌” AND “函館”) AND “日本料理”

イ　(“札幌” AND “函館”) OR “日本料理”

ウ　(“札幌” OR “函館”) AND “日本料理”

エ　(“札幌” OR “函館”) OR “日本料理”

正解　ウ

この問題は集合演算の「分配法則」を使うことで数学的に解くことも可能です。ただし，講義動画でも説明していませんし，ITパスポート試験のレベルを超えてしまう内容ですので，今回は消去法を使って解いてみます。

アは「札幌と函館の両方にあり，かつ日本料理の店」という条件になっています。これだと札幌か函館の片方にしかないお店が検索できませんので正解ではありません。

イは「札幌と函館の両方にあるか，もしくは日本料理の店」という条件になっています。これだと札幌と函館の両方にあれば日本料理の店じゃなくても検索できてしまいますし，日本料理の店であれば札幌と函館に関係なく検索できてしまいますので正解ではありません。

ウは「札幌または函館にあり，かつ日本料理の店」という条件です。この条件であれば札幌にある日本料理の店も函館にある日本料理の店も検索できますので，これが正解です。

エは「札幌または函館にあるか，もしくは日本料理の店」という条件になっています。これだと札幌または函館にあれば日本料理の店じゃなくても検索できてしまいますし，日本料理の店であれば札幌と函館に関係なく検索できてしまいますので正解ではありません。

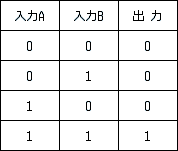
真理値表に対応する論理演算はどれか。(IP_H24秋_問82)

ア　AND

イ　NOT

ウ　OR

エ　XOR

正解　ア

入力Aと入力Bの両方が1(真)のとき，出力が1(真)になっています。これはAND(論理積)の特徴です。

覚えていないと解けませんので，ORとXORも含めてしっかりと覚えておいてくださいね。