貴方の成長を手助けする無料ＩＴ資格スクール

X社では来期に製品A，B，C，Dのいずれか一つを市場に投入することを検討している。来期の市況で好況の確率は40％，不況の確率は60％と予想され，市況ごとの各製品の予想売上高が表のとおりであるとき，この市場から得られる最大の売上期待値をもたらす製品はどれか。(IP_H23春_問26)

ア　製品A

イ　製品B

ウ　製品C

エ　製品D

正解　イ

最大の売上期待値をもたらす製品はどれかということなので，実際に各製品の売上期待値を計算します。

期待値は各値に確率を掛けたものを合計して求めますので，

好況時の予想売上高×好況の確率＋不況時の予想売上高×不況の確率

で計算します。

製品A：12×0.4＋10×0.6＝4.8＋6.0＝10.8

製品B：18×0.4＋8×0.6＝7.2＋4.8＝12.0

製品C：20×0.4＋6×0.6＝8.0＋3.6＝11.6

製品D：10×0.4＋12×0.6＝4.0＋7.2＝11.2

よって，売上期待値が最大なのは製品Bですね。

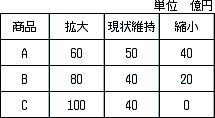
ある市場が今後，拡大，現状維持，縮小する場合の商品A，B，Cの販売利益が表のとおり見込まれており，拡大，現状維持，縮小する確率がそれぞれ0.2，0.5，0.3であるとき，どの商品を販売すると予想利益が最高となるか。ここで，商品の予想利益は販売利益の期待値から開発コストを差し引いたものとし，各商品A，B，Cの開発コストは，それぞれ20億円，10億円，15億円とする。(IP_H22春_問11)

ア　A

イ　B

ウ　C

エ　A，B，Cどれでも同じ

正解　イ

予想利益が最大となる商品を期待値を使って計算します。問題文中に，販売利益の期待値から開発コストを差し引いたものが予想利益とありますので，

(拡大時の販売利益×拡大する確率＋現状維持時の販売利益×現状維持の確率＋縮小時の販売利益×縮小する確率)−各商品の開発コスト

で計算します。

商品A：(60×0.2＋50×0.5＋40×0.3)−20＝(12＋25＋12)−20＝29

商品B：(80×0.2＋40×0.5＋20×0.3)−10＝(16＋20＋6)−10＝32

商品C：(100×0.2＋40×0.5＋20×0)−15＝(20＋20)−15＝25

よって，予想利益が最高となるのは商品Bですね。